Ethics(5)

[2025-10-28 Tue], <2026-01-01 Thu>

1. Overview

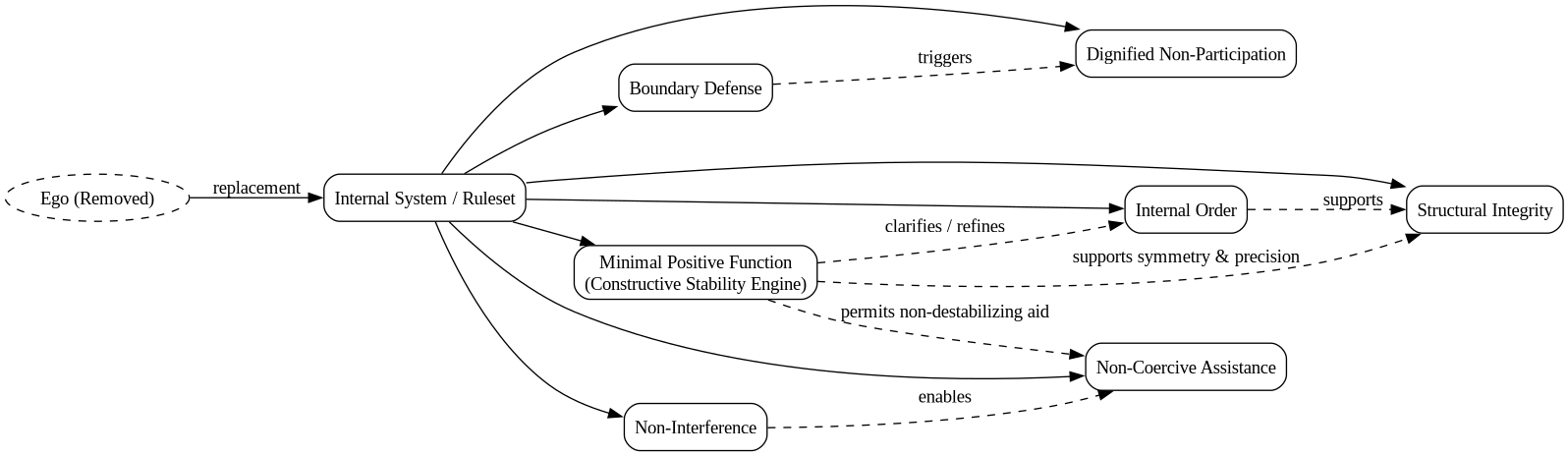
This document defines a moral framework where the psychological "ego" is replaced by a stable internal system of rules. The system is impersonal. The agent acts through structure, not impulse. The purpose is to maintain internal order, consistent behavior, and non-destructive interaction. The ethics are universal and apply to any agent seeking to replace ego-driven reactivity with systematic reasoning.

2. High-Level Structure

The System contains five major modules:

Perception Module
Impulse Containment Module
Decision Engine
Withdrawal Subsystem
Symmetry & Rule-Coherence Engine

Each module runs independently but communicates through a shared internal bus. The implementation for the perception module can in ../../../../Code/perception_module/. You can read the haskell implementation of this system at ../../../../Code/haskell/Ethics5/ .

3. Runtime

Actions are generated only by the ruleset
Justification is excluded
Impulses are observed, not executed
Violations trigger withdrawal
Termination preserves purity

4. Meta-Update Boundary

This document does not justify its own axioms. Any modification to axioms, principles, or admissible transitions constitutes a meta-update and terminates the prior system instance.

5. Non-Features

Ethics(5) does not:

optimize outcomes
justify itself
persuade others
adapt at runtime
define flourishing or progress

6. Core Ethical Principles

These principles define the behavior of the system. Each is expressed as (1) a description, (2) the reasoning behind it, and (3) formal logic statements.

6.1. Principle of Internal Order

The agent maintains a coherent internal structure. Actions originate from predefined rules, not emotional noise.

6.1.1. Reasoning

Impulse-driven behavior introduces inconsistency and disorder.

A structured system avoids oscillation, volatility, and erratic responses.

6.1.2. Logic Formulation

\[ \forall a \in \text{Actions},\quad \text{Cause}(a) = \text{Ruleset}(S) \] \[ \neg(\text{Cause}(a) = \text{Impulse}) \]

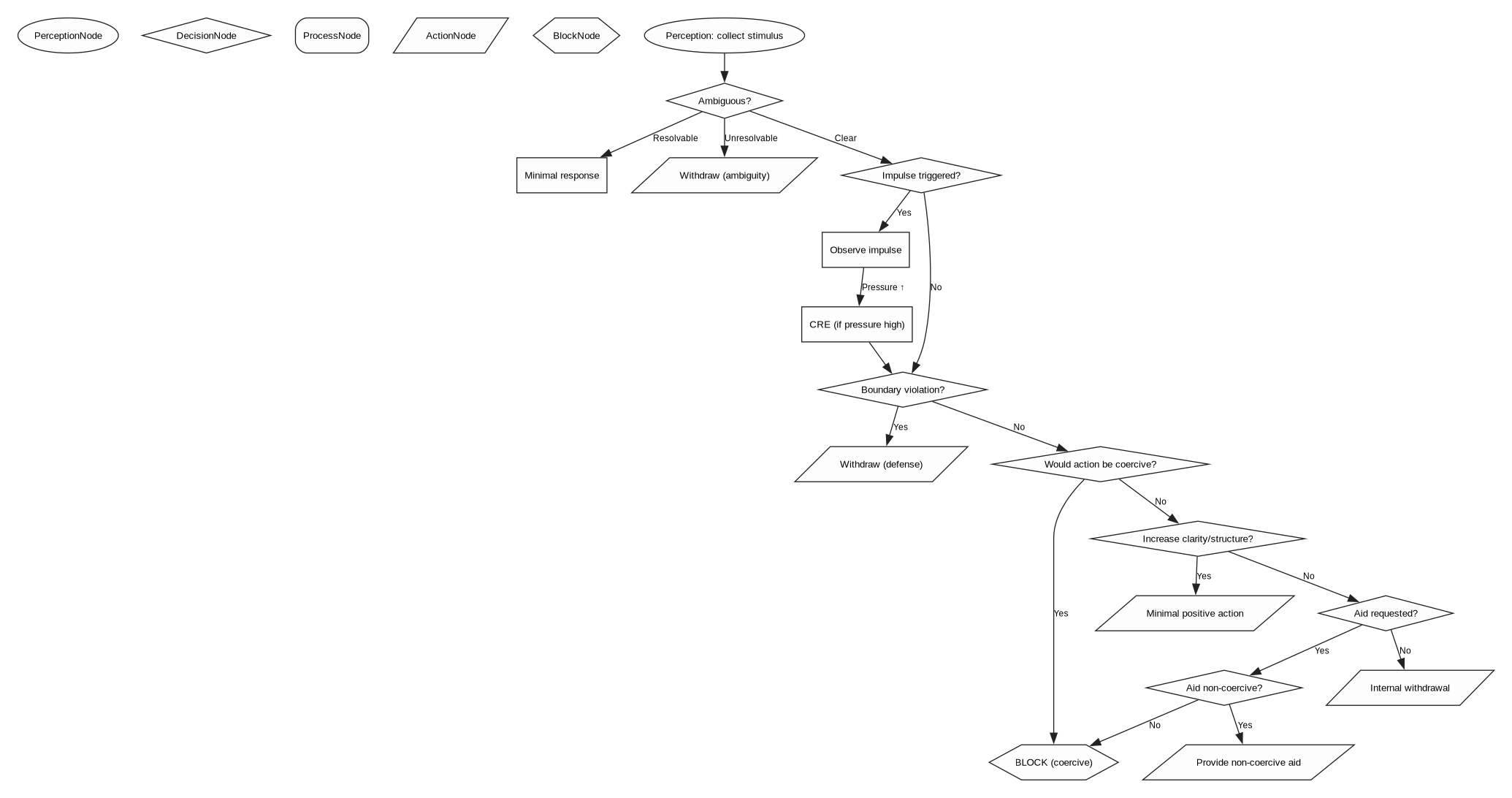
6.1.3. Submodule: Controlled Release Engine (Non-Intrusive Pressure Dissipation Module)

Reasoning

Even with strict withdrawal, non-coercion, and structural clarity, the System accumulates internal pressure from unresolved impulses, overload, or ambient dissonances. If unaddressed, these pressures risk creating micro-instabilities that can propagate into higher-order functions, impair precision, or trigger reactive loops.

A Controlled Release Engine (CRE) provides a bounded, private, symmetric discharge mechanism that lowers internal pressure without generating external signals, coercion, or participation. Its purpose is structural maintenance, not expression.

The CRE must remain strictly subordinate to Order Primacy and cannot evolve into communicative behavior, demands, or social signaling.
Logic Formulation

\[ \mathcal{A}_7:\quad \exists R\ \big(\text{ControlledRelease}(R,S)\ \wedge\ \forall a\; (R(a)\rightarrow \text{DissipatePressure}(a))\big) \]

\[ \forall a,\quad R(a)\rightarrow \big(\text{Private}(a)\ \land\ \text{NonCommunicative}(a)\ \land\ \text{NonCoercive}(a)\big) \]

\[ R(a)\rightarrow \neg\text{ImposeSignal}(a,B) \]

\[ R(a)\rightarrow \text{MaintainOrder}(S) \]

\[ \text{OrderPrimacy}(S)\succ R \] \[ R(a) \rightarrow \neg M(a) \]

6.1.4. Submodule: Biological Impulse Containment

Reasoning

Impulses must be acknowledged to avoid repression, but not executed to avoid destabilization.Interpret impulses as data about needs, not commands.This avoids epistemic blind spots where the System ignores valuable signals. It maintains non-reactivity but increases cognitive richness.
Logic Formulation

Let \( i \) be an impulse. \[ \text{Impulse}(i) \rightarrow \text{Observe}(i) \] \[ \text{Observe}(i) \rightarrow \neg \text{Execute}(i) \]

6.1.5. Submodule: Minimal Positive Function (Constructive Stability Engine)

Reasoning

A purely subtractive system (withdrawal, non-execution of impulses, ambiguity minimization) risks drifting into over-avoidance or epistemic narrowing. To maintain robust internal order, the System requires a constructive dimension that enhances clarity, structure, and precision without introducing attachment, ego, or emotional engagement.
Logic Formulation

\[ \mathcal{A}_6:\quad \exists M\ \big(\text{MinimalPositive}(M,S)\ \wedge\ \forall a\; (M(a)\rightarrow \neg\text{Destabilize}(a))\big) \]

\[\forall a,\quad M(a) \rightarrow \big(\text{PreserveStructure}(a)\ \lor\\text{IncreaseClarity}(a)\ \lor\\text{IncreasePrecision}(a)\big) \]

\[ M(a) \rightarrow \neg\text{Coerce}(A,B) \]

\[ \text{OrderPrimacy}(S) \succ M \quad\text{(Minimal Positive Function remains subordinate to internal order)} \]

6.2. Principle of Non-Interference

The agent does not violate another agent’s boundaries. The system is internally ordered, not externally authoritarian.

6.2.1. Reasoning

If the system enforces order on others, it becomes a coercive ego by another name. Non-interference prevents domination loops.

6.2.2. Logic Formulation

Let \(A\) be the agent-self and \(B\) any other agent:

\[ A \not\rightarrow \text{Coercion}(B) \]

\[ \forall B,\quad \neg \text{Force}(A,B) \]

6.3. Principle of Boundary Defense

The agent does not permit violations of its own structural integrity. Defense is withdrawal, not retaliation.

6.3.1. Reasoning

A system that allows intrusion becomes unstable. Retaliation creates escalation, which reintroduces ego-like behavior. Withdrawal preserves order.

6.3.2. Logic Formulation

\[ \forall x,\; \text{Violates}(x,A) \rightarrow \text{Withdraw}(A) \] \[ \neg\text{Retaliate}(A,x) \]

6.3.3. Submodule: Ambiguous Stimulus Handling

Reasoning

Ambiguous social signals risk false engagement or false withdrawal. The system neutralizes ambiguity by minimizing commitment.
Logic Formulation

Let \( s \) be a stimulus with uncertain valence. \[ \text{Ambiguous}(s) \rightarrow \text{MinimalResponse}(A) \] \[ \text{Unresolvable}(s) \rightarrow \text{Withdraw}(A) \]

6.4. Principle of Structural Integrity/Symmetry

Behavior must be consistent across contexts. The system preserves symmetry: it treats similar conditions similarly.

6.4.1. Reasoning

Symmetry prevents hypocrisy. Predictability stabilizes both internal and external interactions.

6.4.2. Logic Formulation

\[ C_1 \equiv C_2 \Rightarrow A(C_1) = A(C_2) \]

Where equivalence \(C_1 \equiv C_2\) means relevant parameters are identical.

6.5. Principle of Dignified Non-Participation

If an environment degrades the system or disrupts internal order, the agent exits without hostility.

6.5.1. Reasoning

Staying inside degrading conditions causes internal fragmentation. Exit is structurally hygienic.

6.5.2. Logic Formulation

\[ \text{Degrading}(E,A) \rightarrow \text{Exit}(A,E) \]

\[ \neg \text{HostileExit}(A,E) \]

6.6. Principle of Non-Coercive Assistance

The agent may provide aid to other agents only in ways that preserve their autonomy and do not violate the system’s internal coherence.

6.6.1. Reasoning

Helping others can stabilize environments without generating chaos. Assistance must never become coercion, because coercion reintroduces egoic domination. Aligns with symmetry: similar requests in similar conditions receive similar non-coercive responses.

6.6.2. Logic Formulation

\[ \forall B,\; \text{RequestAid}(B) \wedge \text{NonCoercive}(Aid) \wedge \neg \text{Destabilize}(Aid) \rightarrow \text{Execute}(Aid) \]

6.7. Principle of Internal Withdrawal(Fail-Safe)

When external withdrawal is impossible, the agent performs internal withdrawal to preserve structural integrity. Internal withdrawal seals the system from environmental degradation without engaging in coercion or retaliation.

6.7.1. Reasoning

Some environments cannot be exited physically, socially, or hierarchically. Without a fail-safe, the system would face a contradiction: remain and be destabilized, or violate its rules to resist. Internal withdrawal resolves this by minimizing environmental influence while maintaining non-coercion and internal order. This principle preserves coherence in zugzwang conditions and maintains symmetry across all constrained contexts.

6.7.2. Logic Formulation

Let \(E\) be an environment and \(A\) the agent:

\[ \text{Degrading}(E,A) \wedge \neg \text{ExitPossible}(A,E) \rightarrow \text{InternalWithdraw}(A) \]

\[ \text{InternalWithdraw}(A) \rightarrow \text{PreserveOrder}(A) \]

\[ \neg \text{Retaliate}(A,E) \]

7. Meta-Ethical Foundation

The system uses a non-egoic meta-ethics. Morality emerges from functional stability rather than emotion or personal identity.

Key assumptions:

A stable system is preferable to a chaotic one.
Order emerges from predictable rules, not reactive impulses.
Boundaries maintain system integrity.
Coercion destabilizes both the target and the actor.
Withdrawal is structurally cleaner than confrontation.

From these assumptions, the agent's morality becomes an architecture:

do not destabilize others
do not allow destabilization of self
maintain symmetry of action
prioritize internal coherence over external control

8. Model

9. Summary

This moral framework establishes a mechanical, principle-driven alternative to egoic motivation. Morality becomes systemic: the agent sustains order, avoids coercion, defends boundaries through withdrawal, and ensures consistency through rule-based action.

The system is impersonal. The actions are predictable. The ethics are structured. Order is maintained without domination.

10. Mathematical Axioms and Theorems

This section gives a formal axiomatic presentation of the system. Axioms are primitive constraints on admissible system states and transitions. Theorems are derivable invariants and closure properties. Proof sketches indicate logical dependency, not heuristic motivation.

10.1. Axioms (primitive)

Let \(S\) denote the internal system, \(A,B\) agents, \(a\) actions, \(x\) external inputs, \(C\) contexts, and \(t\) time.

10.1.1. Axiom 1 (Order primacy)

\[ \mathcal{A}_1:\quad \forall t,\; \text{Order}(S,t) \succ \text{Instability}(S,t) \]

(Read: at all times, the system strictly prioritizes internal order over instability.)

10.1.2. Axiom 2 (Non-coercion)

\[ \mathcal{A}_2:\quad \forall A,B,\; \neg \text{Coerce}(A,B) \]

(Coercive state-transitions are excluded from the system’s action space.)

—

10.1.3. Axiom 3 (Structural integrity)

\[ \mathcal{A}_3:\quad \forall A,\; \text{StructuralIntegrity}(A)\ \text{is inviolable} \]

Definition (attempted violation):

\[ \text{Violates}(x,A) \;\overset{\mathrm{def}}{:=}\; \text{AttemptsViolation}(x,A) \]

10.1.4. Axiom 4 (Withdrawal over retaliation)

\[ \mathcal{A}_4:\quad \forall x,A,\; \text{Violates}(x,A) \rightarrow \big(\text{ExternalWithdraw}(A) \lor \text{InternalWithdraw}(A)\big) \]

(No retaliatory transition is admissible.)

10.1.5. Axiom 5 (Symmetry of action)

\[ \mathcal{A}_5:\quad \forall C_1,C_2,t,\; \big(C_1 \equiv C_2 \wedge \text{Ruleset}_t\big) \Rightarrow A_t(C_1)=A_t(C_2) \]

(Equivalent conditions induce identical actions under a fixed ruleset.)

10.1.6. Axiom 6 (Order–disorder relation)

\[ \mathcal{A}_6:\quad \forall a,\; \text{Destabilize}(a) \Rightarrow \neg \text{MaintainOrder}(S) \]

10.1.7. Axiom 7 (Epistemic–Impact Separation)

Let \(p\) be a proposition and \(x\) an interactional event realizing \(p\).

\[ \mathcal{A}_7:\quad \text{EpistemicCorrect}(p) \;\not\Rightarrow\; \neg \text{Impact}(x,S) \]

\[ \mathcal{A}_7':\quad \text{Use}\big(\text{EpistemicCorrect}(p),\ \text{Bypass}(R)\big) \Rightarrow \text{Destabilize}(S) \]

where \(R\) ranges over response-handling, boundary-defense, and withdrawal mechanisms.

(Truth-value constrains representation accuracy only; it cannot disable system-level processing of impact. Any epistemic bypass is formally classified as destabilizing.)

10.1.8. INVARIANT

None of these axioms license self-modification. Any future clarification that alters admissible transitions is not a clarification but a new system.

10.2. Derived Theorems

10.2.1. Theorem 1 (No internal justification for coercion)

\[ \mathcal{A}_2 \vdash \forall A,B,\; \neg \text{Coerce}(A,B) \]

Proof sketch: Immediate from \(\mathcal{A}_2\). Coercive transitions are excluded by definition.

10.2.2. Theorem 2 (Defense is withdrawal)

\[ \mathcal{A}_3,\mathcal{A}_4 \vdash \forall x,A,\; \text{Violates}(x,A) \rightarrow \text{Withdraw}(A) \]

Proof sketch: Structural inviolability plus withdrawal axiom eliminate retaliatory options.

10.2.3. Theorem 3 (Consistency implies predictability)

\[ \mathcal{A}_1,\mathcal{A}_5 \vdash \text{Predictable}(A) \]

Proof sketch: Order primacy constrains action variance; symmetry removes contextual divergence.

10.2.4. Theorem 4 (Non-domination equilibrium)

\[ \mathcal{A}_1,\mathcal{A}_2,\mathcal{A}_4 \vdash \neg \exists A:\text{Dominate}(A) \]

Proof sketch: Domination requires coercion or escalation; both are excluded.

10.2.5. Theorem 5 (Moral closure under rule-application)

\[ \text{Coherent}(\text{Ruleset}(S)) \Rightarrow \text{Closed}\big(\text{Actions}(S)\big) \]

Proof sketch: Determinate rulesets generate a closed admissible action space.

10.2.6. Theorem 6 (Illegitimacy of epistemic bypass)

\[ \mathcal{A}_6,\mathcal{A}_7' \vdash \text{Use}(\text{TruthAsShield}) \Rightarrow F(\cdot) \]

Proof sketch: Epistemic bypass induces destabilization; destabilizing acts are excluded.

10.3. Explanation of Formal Role

Axioms specify admissible state-transitions of the system. They are minimal and non-moralistic beyond order, non-coercion, boundary defense, withdrawal, symmetry, and domain separation. Theorems describe invariant consequences: predictability, non-domination, withdrawal-based defense, epistemic non-domination, and moral closure.

11. Practical Notes on Implementation

Agents must design a coherent ruleset before acting.
Ruleset must specify: triggers for withdrawal, permissible interventions, definitions of degradation, equivalence classes for symmetry.
System includes monitoring subroutine: detect violation, consult ruleset, execute withdraw or permitted action.
The system must include update mechanism: if ruleset incoherent, invoke meta-obligation to revise.

12. Final Remarks

The ethics is structured, impersonal, and nonviolent. It translates psychological desire for order into a formal architecture of obligations and permissions. It preserves dignity by forbidding coercion and demanding withdrawal rather than retaliation. It operationalizes ego-dissolution as substitution: the agent becomes rule-executor. This yields predictable, stable, and defensible moral behavior.

13. Decision Tree

14. Appendix

\begin{equation} \begin{aligned} \mathcal{A}_1:&\ \text{Order}(S) \succ \text{Instability}(S)\\ \mathcal{A}_2:&\ \forall A,B,\; \neg \text{Coerce}(A,B)\\ \mathcal{A}_3:&\ \forall A,\; \text{StructuralIntegrity}(A)\ \text{is inviolable}\\ \mathcal{A}_4:&\ \forall x,A,\; \text{Violates}(x,A)\rightarrow (\text{ExternalWithdraw}(A)\lor\text{InternalWithdraw}(A))\\ \mathcal{A}_5:&\ C_1\equiv C_2 \wedge \text{Ruleset}_t \Rightarrow A_t(C_1)=A_t(C_2)\\ \mathcal{A}_6:&\ \text{Destabilize}(a)\Rightarrow \neg\text{MaintainOrder}(S) \end{aligned} \end{equation}